Handeling hierarchical data

I am analyzing leafing time data with a hierarchical structure, where each observation is associated with a specific year and individual.

The simplest approach is to ignore this structure and fit a standard regression to all data, a completely pooled model.

Completely pooled

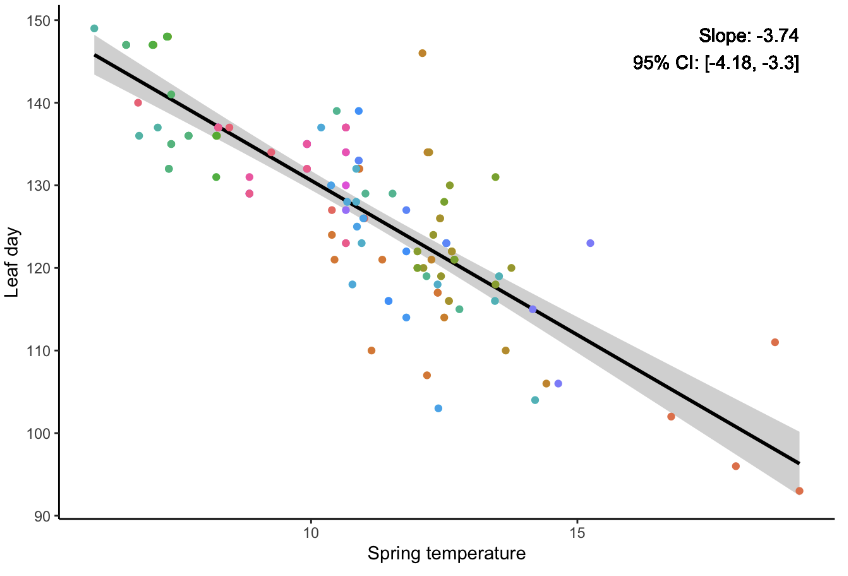
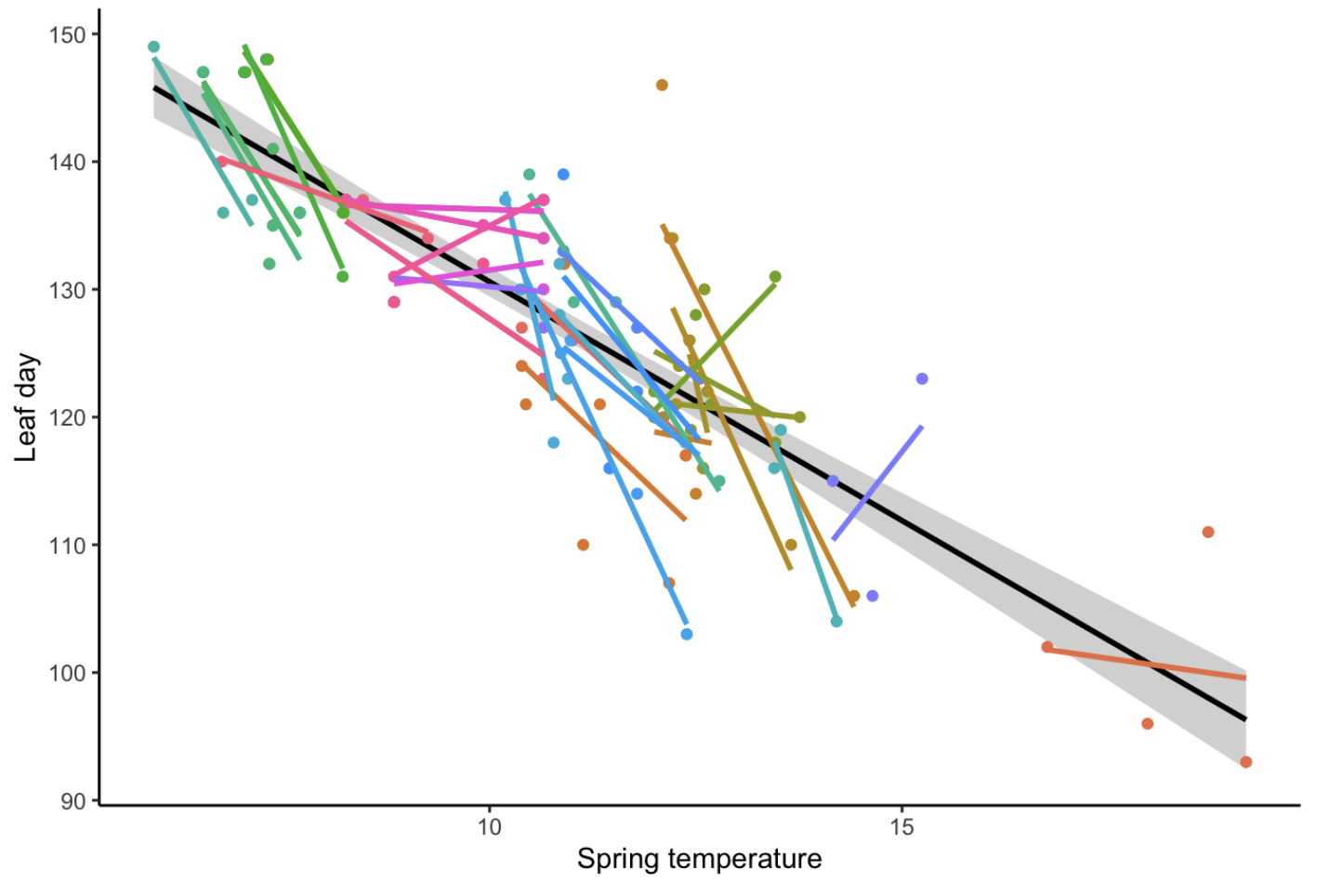
Alternatively, we can fit a separate model for each individual, known as a completely unpooled model.

Completely unpooled

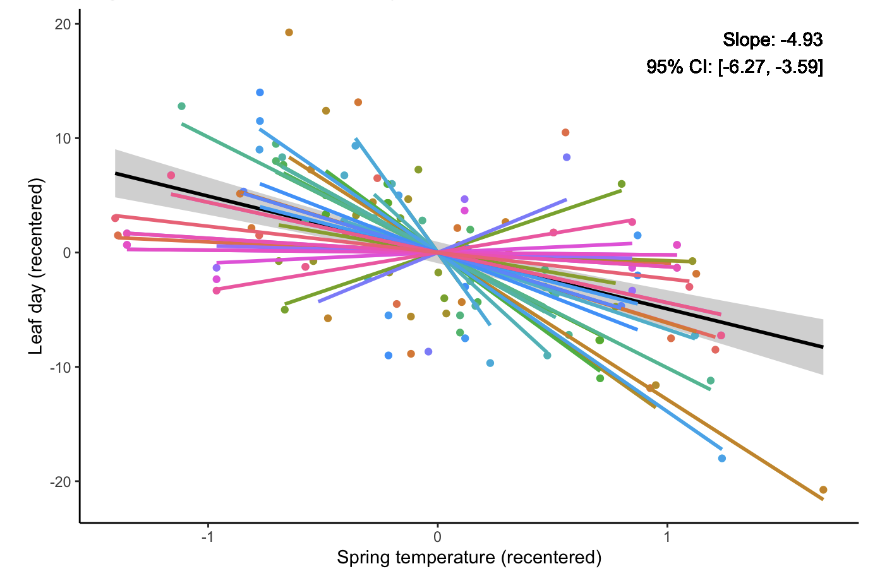
A third common approach is to recenter the group-level data.

Recentered model

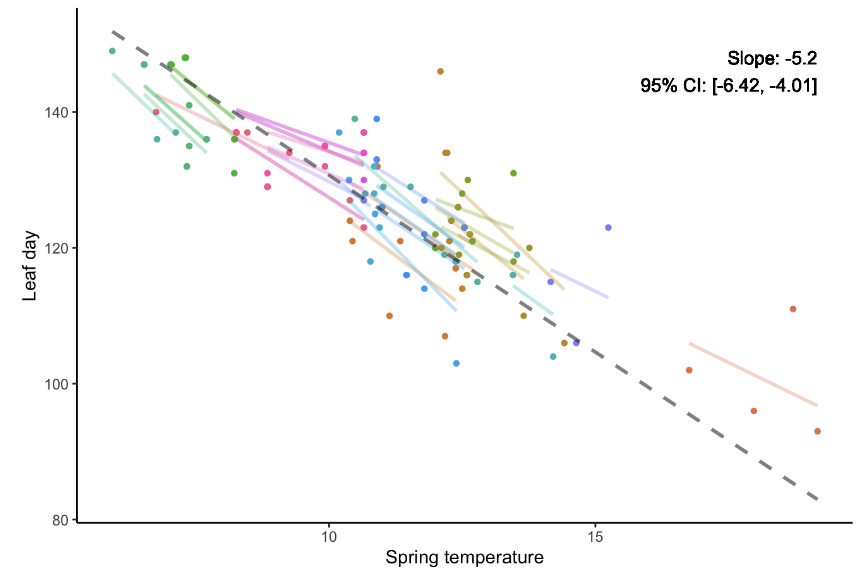
But a better strategy is the partially pooled model (such as a mixed-effects model), which allows for group-specific effects while also sharing information across groups through shared hyperparameters.

Partially pooled

Here, we are going to talk a little bit about the connection between a completely unpooled model and two versions of partially pooled models.

Unpooled

In short, the difference lies in how we define the relationship among the group-level parameters. If they are completely independent, the model is completely unpooled; if they are exactly identical, the model is completely pooled.

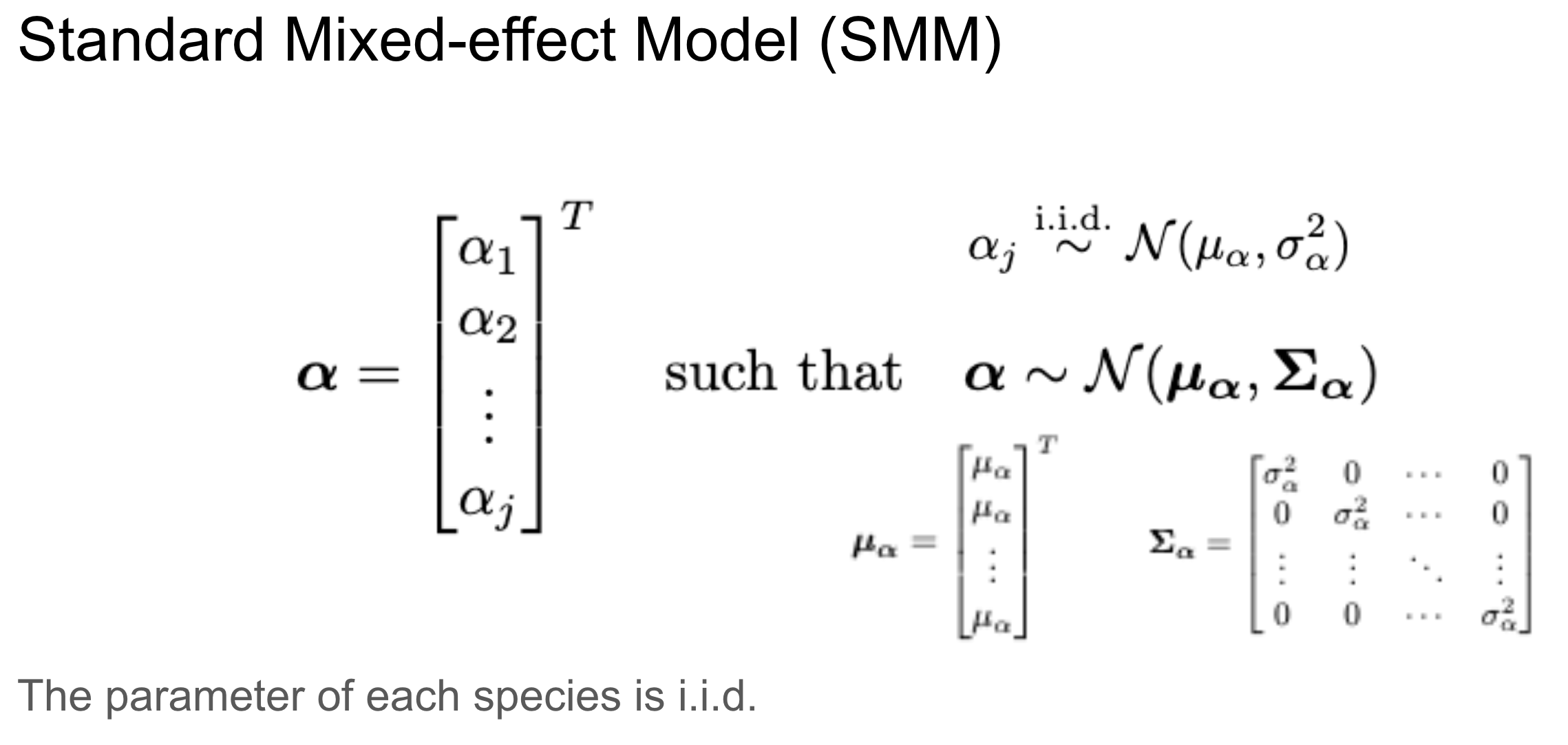
SMM

A standard mixed-effects model constrains the group-level parameters with a normal distribution.

This can also be written as a multivariate normal distribution, which allows for more fine-tuning.

PMM

One such fine-tuning is to incorporate phylogenetic data, assuming that species closer in evolutionary history should be more highly correlated in this trait.

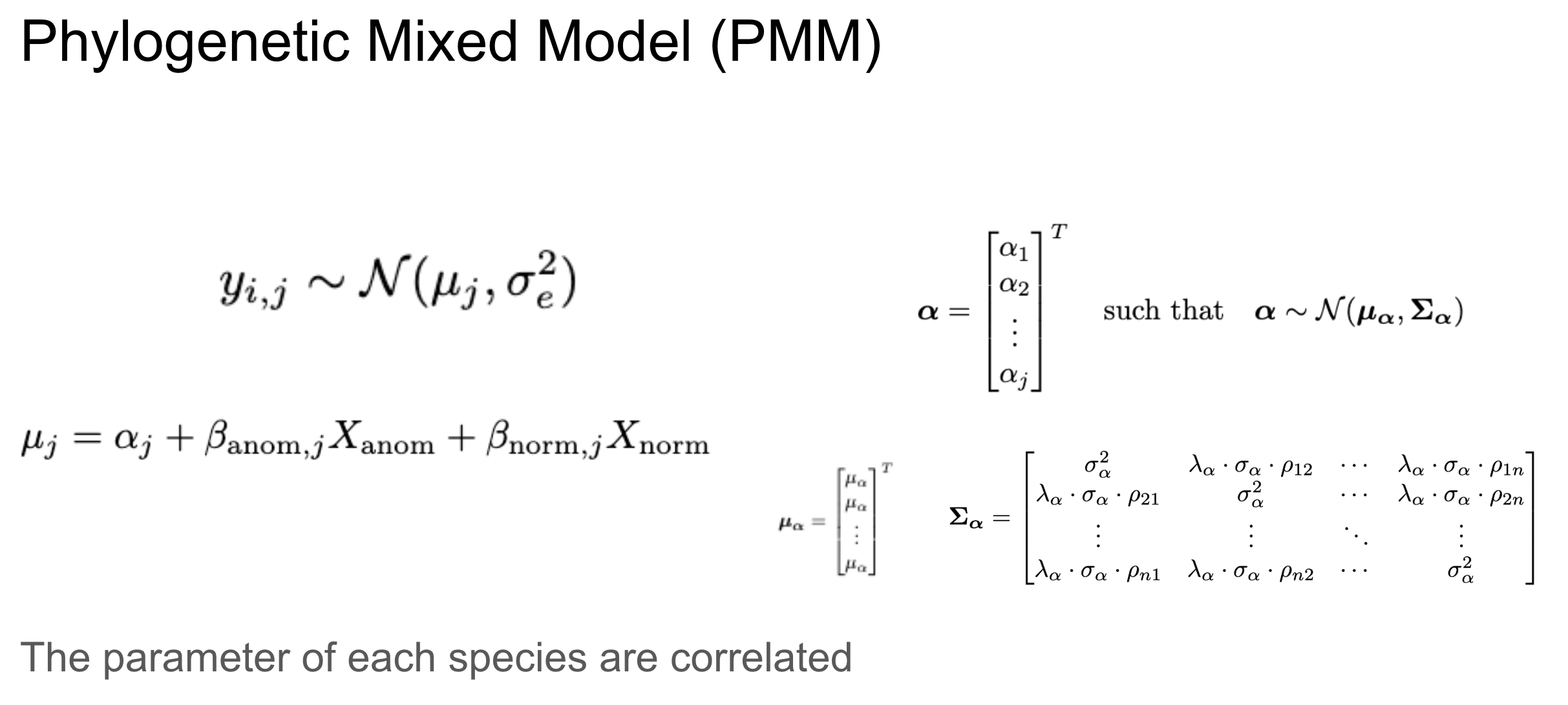
𝜌 is the shared life history. Pagel’s 𝜆 is the phylogenetic signal.